Bullet Stability

Why are barrels rifled? Why not use a smooth bore? It would certainly simplify things for the barrel manufacturer and lower costs for everyone.

The answer is that bullets will not fly straight unless you spin them. The rifling grips the bullet by the jacket and forces it to spin at a high rate as it is pushed down the bore by propellant gasses. Rifling ensures bullets will be stable.

Defining Stability

But let's back up a little bit. What does it mean to be stable? Simply put, it means the bullet's nose is pointed into the air flow. If you look at a rocket or missile, you'll notice that many designs have fins at the rear. Those fins are there to ensure that the front of rocket points forward. They work like a weather vane - if the rocket starts to tip, the airflow pushes on the fins, correcting the alignment. Whenever there is a non-zero yaw, there is also a force present to correct it - the air flow blowing on the side of the fin.

Bullets, of course, do not have fins. In theory, you could make finned bullets, but it would be very difficult and expensive. Instead, we spin bullets to create a similar effect. Because of the physics of spinning objects, which I'll skip, when a bullet is spinning and it starts to yaw, there are forces that tend to automatically correct the orientation. It turns out that bullets do not perfectly stabilize (there is always some yaw present), but you can get them close enough.

There are two kinds of bullet stability that we are concerned about - gyroscopic stability and dynamic stability. For a bullet to be stable, both conditions must be met - a bullet that is gyroscopically stable but dynamically unstable is not stable - it will tumble.

Gyroscopic Stability

Gyroscopic stability is the easier of the two to understand. Gyroscopic stability is usually referred to as a variable called Sg. Mathematically speaking, if Sg is greater than 1.0, the bullet can be said to be gyroscopically sable. Sg goes up if you spin the bullet faster. Sg also goes up if velocity decreases. Sg goes down if you use a longer, thinner bullet. If a bullet starts out gyroscopically stable, it tends to stay that way because velocity drops faster than the bullet's spin rate. If a bullet is gyroscopically unstable at the muzzle, it will never be stable.

Factors That Increase Gyroscopic Stability

• Lower velocity
• Higher spin rate
• Shorter/fatter bullet geometry
• Lower air density

While calculating Sg is not terribly complex, it's not the sort of thing you can do with a hand calculator except as an approximation. That is a topic for another article. There are several calculators available on the web that will give you an approximate value, however, such as this one by JBM Ballistics.

Dynamic Stability

Dynamic Stability is much tougher to calculate. It depends on obscure coefficients that are hard to pin down. It's difficult to predict, and depends on subtle features of the bullet's design. Bullets can lose dynamical stability as they lose velocity. Unlike the case with gyroscopic stability, stability at the muzzle does not imply stability down range. Dynamic stability is referred to by a variable called Sd. Calculating the exact number is beyond the scope of this article - just know that it is hard to predict and requires a lot of data.

A bullet with "perfect" dynamic stability will have a Sd equal to 1.0. If Sd is less than or greater than 1.0, the bullet may become unstable. The safety margin for Sd depends on Sg. A bullet with a high Sg has more padding when it comes to Sd. A bullet that is on the ragged edge of gyroscopic stability will become dynamically unstable very easily.

Putting It Together

Skipping the math, we wind up with the following relationship between Sg, Sd and bullet stability:

A bullet is stable if:

If you plot that on a graph, you wind up with the following chart:

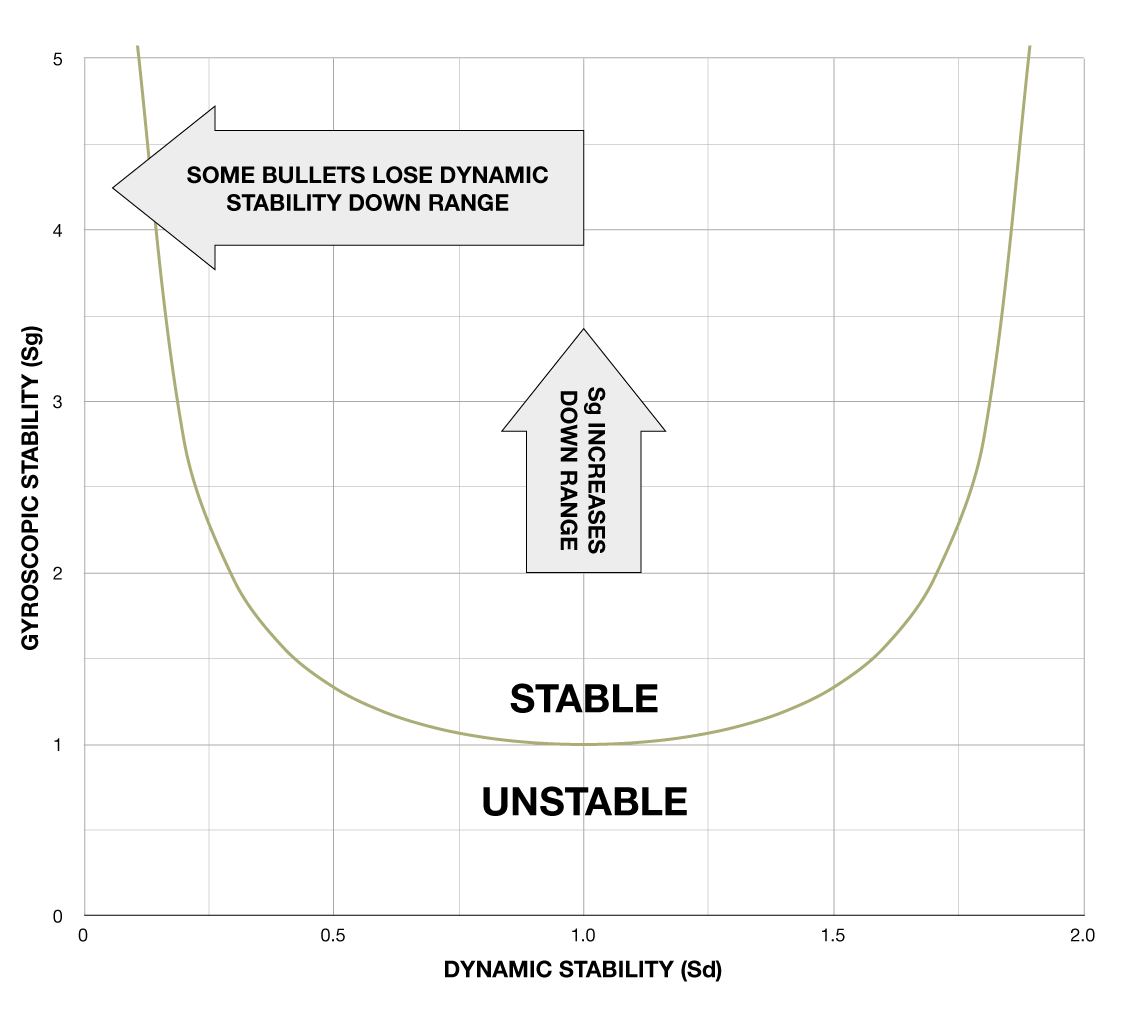
As you can see, there are two regions divided by the line represented by the above equation. If a bullet is inside the stable region, all is good. If it leaves the stable region, it will tumble.

A well behaved bullet will begin its flight on the center line (Sd = 1.0) and move up as it heads down range. Again, this is because the bullet's spin will decay at a slower rate than it's velocity, which will lead to a higher gyroscopic stability. This is what we want.

However, dynamic stability is not as, well, stable. Further down range, some bullets will experience a dramatic shift in Sd, which can cause the bullet to leave the stable region and begin to tumble. The infamous .30 caliber 168 grain Sierra MatchKing suffers from this problem, and is prone to losing stability at transonic velocities. This is one reason that long range shooters like to keep velocities over 1,300 feet per second at the target. Bullets that tend to lose stability do so in the transonic region.

Atmospheric Effects

Further complicating matters is that all of this depends on air density, which is in turn dependent on things like altitude, temperature, and humidity. Lower air density means greater stability. Think of it this way - there is less air to cause the bullet to tumble. So it's possible to have a bullet shoot well at high altitude, but tumble at sea level.

Practical Takeaway

Bullet stability is only partially in the hands of the shooter. The only thing you can really do is to choose bullets that will be adequately stabilized by your rifle's barrel twist. Always choose a bullet/barrel combination that will produce an Sg of at least 1.3 to 1.4 in order to provide some margin against dynamic instability and atmospheric conditions. Going higher than that will not cause huge problems, but keep in mind that increasing spin has an adverse effect on accuracy, so there is a balance to maintain between stability and accuracy. Use the minimum twist that will stabilize the heaviest bullets you want to shoot.

Unfortunately, there is little that can be done about dynamic stability problems outside of avoiding bullets that exhibit problematic behavior. And the only way to know which bullets to avoid is to ask around. Most bullets used for long range shooting are good if you keep them moving fast enough. Trouble begins when you start to dip into the transonic region, which most long range shooters avoid if at all possible. If you find your bullets dropping that much velocity, maybe you need a bigger cartridge. This is usually only a problem for competition shooters who are restricted to certain cartridges, as in F Class T/R competition, which requires .308 Winchester or .223 Remington.

Update - 10/4/14

While the above recommendations are still applicable at short range, there is a section in Bryan Litz's new book, Modern Advancements in Long Range Shooting, that details his experiments with drag and stability. He presents a compelling argument that there is a slight increase in drag when Sg falls below approximately 1.5. Noting that, I now think it prudent to use at least a 1.5 stability factor for long range shooting, where the slight degrease in drag is more important than the slightly decreased accuracy from over-spinning the bullet. For very high precision, short range applications (basically short range benchrest), it may be desirable to use the bare minimum stability you can get away with, but keep it over 1.5 for long range. As far as I know, this represents the latest thinking/research in this area.

Further Reading

This article only scratches the surface of bullet stability. For the mathematically inclined, Bob McCoy's book, Modern Exterior Ballistics, delves into the arcane mathematical details. For a broader, less technical overview, Bryan Litz's Applied Ballistics for Long-Range Shooting is an excellent resource.

Damon Cali is the creator of the Bison Ballistics website and a high power rifle shooter currently living in Nebraska.