Barrel Twist and Bullet Stability

The barrel twist you choose for your rifle can have a significant impact on it's accuracy. But how and why?

Bullet Stability

Bullets are aerodynamically unstable. Left to their own devices, they will tumble through the air in an accuracy destroying, chaotic manner, hitting the target in a basically random orientation - straight, sideways, or even backwards. If you spin them at a high rate, however, they behave quite nicely, and will keep their nose pointed more or less down range.

The longer the bullet, the more spin it needs. Accurately calculating the amount of spin required to stabilize a given bullet requires the use of some empirically derived constants, not unlike the ballistic coefficient we're all familiar with. Those constants are not generally available. For the mathematically inclined, a more thorough treatment of the math behind bullet stability can be found in Robert McCoy's excellent Modern Exterior Ballistics: The Launch and Flight Dynamics of Symmetric Projectiles - but only if you have a heavy duty math background (a math or engineering degree or equivalent knowledge).

For the less eager, there are several approximate methods of calculating the required spin for a bullet. The simplest is the old Greenhill formula:

T = 150 / L

where T is the twist in bullet calibers, and L is the length of the bullet in calibers.

Unfortunately, it's not a very good method, but I include it here to show that longer bullets require faster twists, which is basically all you need to know. A better calculator that uses a more involved method is available at JBM Ballistics.

So why not just pick a really fast twist and be done with it? It turns out the very spin that keeps our bullets stable also conspires to send our shots off target - it is possible to over-spin a bullet.

Bullet Balance

Perfect bullets are balanced both statically and dynamically. That is, the bullet's center of gravity is on the bullet's axis of symmetry (static balance) and the bullet's principal axis of inertia is parallel to the bullet's axis of symmetry (dynamic balance). Static balance is straightforward enough, but what is this principal axis business?

Think of a tire being balanced - the goal is to add weights until the wheel's principal axis of inertia aligns with the wheel's physical axle. if they are not in line, the wheel will wobble. The same thing happens with bullets.

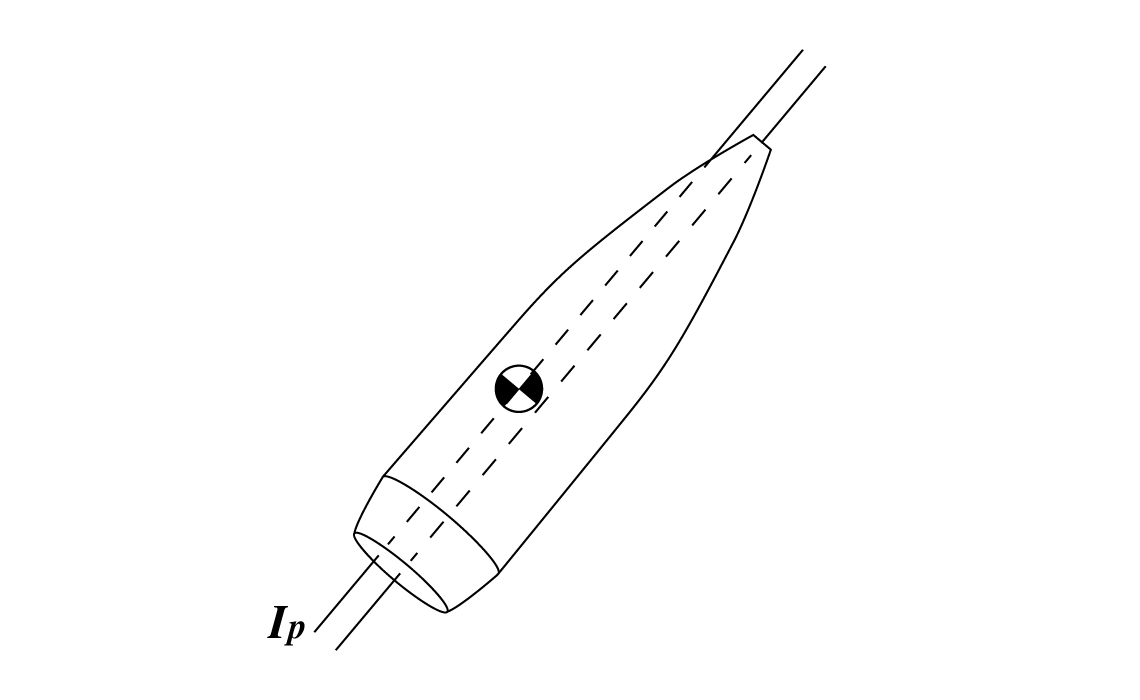
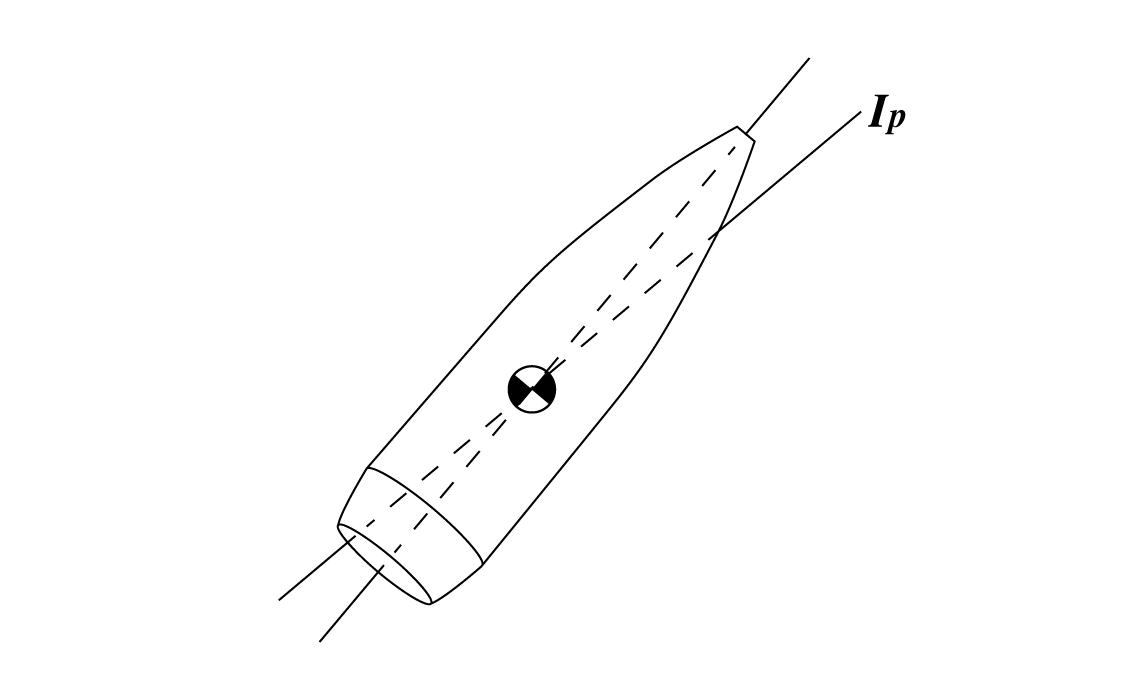
In real life, all bullets have both static and dynamic imbalance. Think of a bullet with a small void or impurity off the centerline. That will throw off both the center of gravity and the principal axis of inertia. So why does this matter?

Lateral Throwoff

The first concept to understand is that of lateral throwoff. When a statically imbalanced bullet travels down the bore, the off-center center of gravity will travel in a helical path since the outside edge of the bullet is constrained by the bore. When the bullet leaves the muzzle, it will fly off in a direction tangent to that helical path. The exact direction depends on what direction the heavy side of the bullet happens to be facing when it leaves the muzzle.

Note that a perfect bullet, if it is allowed to tip in the bore, will also fall prey to lateral throwoff. All that is required is for the center of gravity of the bullet to be off the bore's centerline.

The faster the barrel twist, the more lateral throwoff you will have. In other words, faster twists are less accurate with imperfect (that is, real) bullets.

Aerodynamic Jump

Similarly, when dynamically unbalanced bullet (even if it is statically balanced with the center of gravity perfectly centered on the bore) leaves the muzzle, it will do so with an initial yaw that causes it to fly off in the wrong direction. This is called aerodynamic jump.

Like lateral throwoff, aerodynamic jump can also caused by in-bore tipping. As we'll see in a moment, wind can also cause aerodynamic jump.

In any case, the faster the barrel twist, the more aerodynamic jump you will have. Again, the deflection will be in a random direction determined by exactly how the bullet was positioned when it left the muzzle.

Lets take a break and summarize. Spin is required to stabilize bullets in flight. Defects in bullet balance or in-bore tipping will cause lateral throwoff and aerodynamic jump, which will cause the bullet to fly off in an unwanted and unpredictable direction. The faster the barrel twist, the more deviation in the trajectory.

Cover Your Bases

An interesting side note is that aerodynamic jump can partially cancel out lateral throwoff. It turns out that a defect forward of the bullet's center of gravity (that is, at the nose) will cause this cancelation. The same defect aft of the center of gravity (that is, at the base) will cause the two effects to reinforce each other. Benchrest shooters have long known that the bullet's base was more important than the nose. This is one reason. (Obviously, a perfectly balanced bullet is the best case, but if you're going to mangle a bullet, do it at the nose.)

Aerodynamic Jump Caused by the Wind

A cross wind will cause the bullet to yaw to the side as soon as it leaves the muzzle - creating aerodynamic jump. However, unlike the jump caused by bullet imbalance, this yaw is predictable since its source is the direction of the wind. Oddly, what happens is that the wind-based aerodynamic jump causes a vertical deflection of the bullet's point of impact. The stronger the wind, the more the vertical deflection will be.

Note that the magnitude of this effect is not small. A .308 168 grain Sierra MatchKing at 2,600 fps will experience a vertical deflection of approximately 3/8" at 100 yards in a 10 mph cross wind. Compare that to the almost 1" of horizontal wind deflection that you might be more familiar with.

Imagine shooting in very gusty winds with a very accurate rifle. You might wind up with a target that looks something like this:

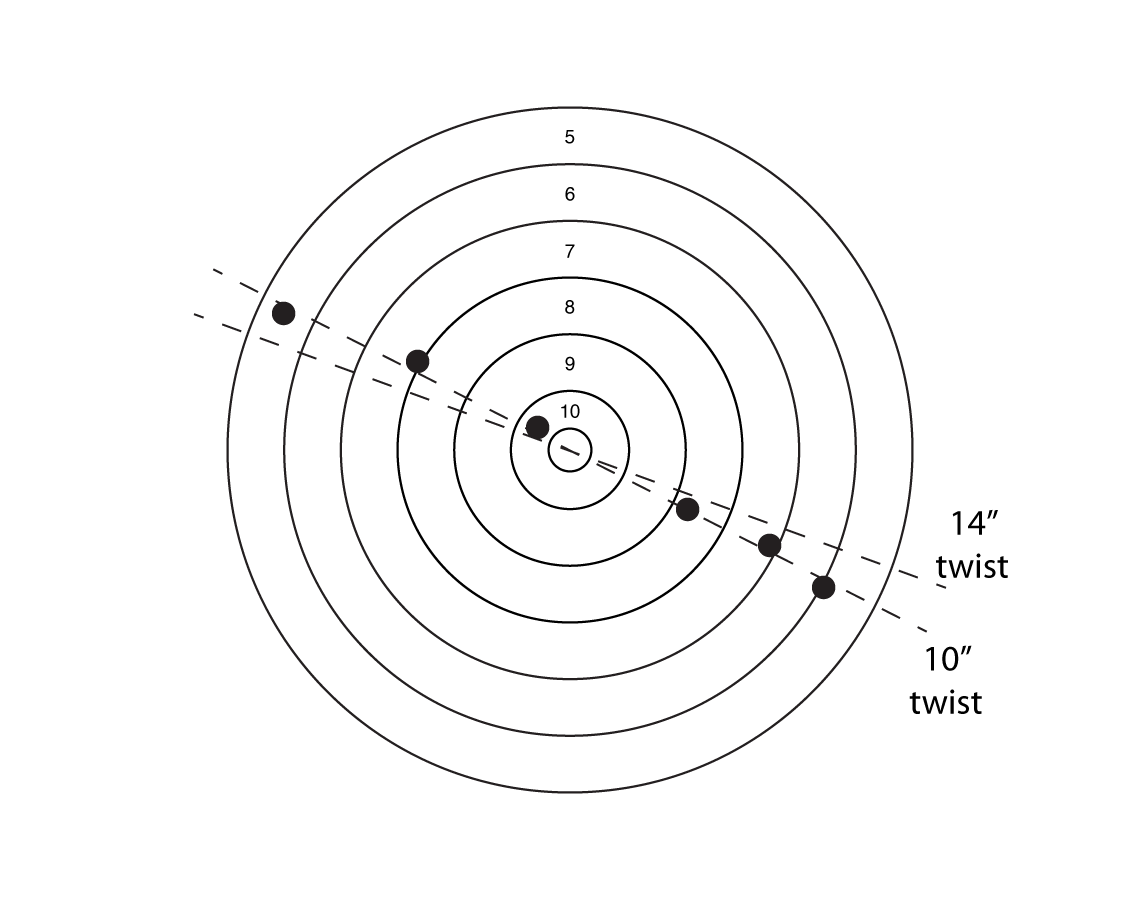
A left to right wind causes bullets to hit low. A right to left wind causes bullets to hit high. (Note that this would be reversed for a rifle with a left hand twist.) So rather than wind causing a pure horizontal dispersion as you might picture, it actually causes a a dispersion at an angle. The faster your rifle's twist, the greater that angle will be.

Now I don't know about you, but it's hard enough for me to keep track of the horizontal impact of the wind without having to worry about a vertical component. By the way, the angles of the lines on the figure are drawn to scale for a Sierra 168 grain MatchKing with a right hand twist at 2,600 fps at 100 yards.

It's important to note that this effect is much more noticeable at short range than long range. This is because the vertical jump is a constant angle no matter the range, while the horizontal wind will increase greatly at longer ranges. So at long range, the ratio of vertical to horizontal deflection will be smaller - that is, the angle of the line in the above chart will not be as steep at long range.

Practical Take-Away

For the highest levels of accuracy, pick a high-quality bullet that will give you acceptable ballistics at the range you need. Then get a barrel with the slowest twist that will stabilize that bullet. Adding a little more twist "just to be sure" will degrade your accuracy by a small amount. Ask around and see what others are using - use the slowest twist that seems to work at the ranges you'll be shooting.

Additionally, we've seen why it's important to keep the bullet aligned with the bore through proper chambering and hand loading techniques, and why we need to pay attention to the wind both at the at the muzzle and down range.

Update - 10/4/14

While the above recommendations are still good guidelines, there is a section in Bryan Litz's new book, Modern Advancements in Long Range Shooting, that details his experiments with drag and stability. He presents a compelling argument that there is a slight increase in drag when Sg falls below approximately 1.5. Noting that, I now think it prudent to use at least a 1.5 stability factor for long range shooting, where the slight degrease in drag is more important than the slightly decreased accuracy from over-spinning the bullet. For very high precision, short range applications (basically short range benchrest), it may be desirable to use the bare minimum stability you can get away with, but keep it over 1.5 for long range. As far as I know, this represents the latest thinking/research in this area.

Damon Cali is the creator of the Bison Ballistics website and a high power rifle shooter currently living in Nebraska.