Case Neck Tension - A Stress Analysis

Handloaders use a lot of words that don't mean anything, and yet they do. Or at least they mean different things to different people. Our craft is littered with words that people have trouble defining - leade, throat, jam, headspace, and yes, neck tension.

SAAMI defines neck tension as "The circumferential stress that the case neck exerts on the seated bullet, as a result of the interference fit provided by the case neck inside diameter and the bullet outside diameter." This is not how any shooter I know defines it, but it hints at what we're after.

There are two commonly used definitions that make sense to me. The first would be the amount of axial force required to push a bullet into or out of a case. That's essentially what we are interested in, but that's not what this article is about. At least, not directly.

The second definition, and the one I'll be using in this article, is the difference between the bullet's diameter and the inside diameter of the sized neck. So if the bullet is 0.308" and the inside of the case neck measures 0.306", you are using 0.002" of neck tension. This shorthand is convenient because it is easy to measure. But what does it mean? How does it relate to the case's grip on the bullet?

Stress, Strength, and Spring-back

If you haven't read my article on annealing, you might want to go do that now, and then come back. Annealing, it turns out, is a pretty important piece of the neck tension puzzle.

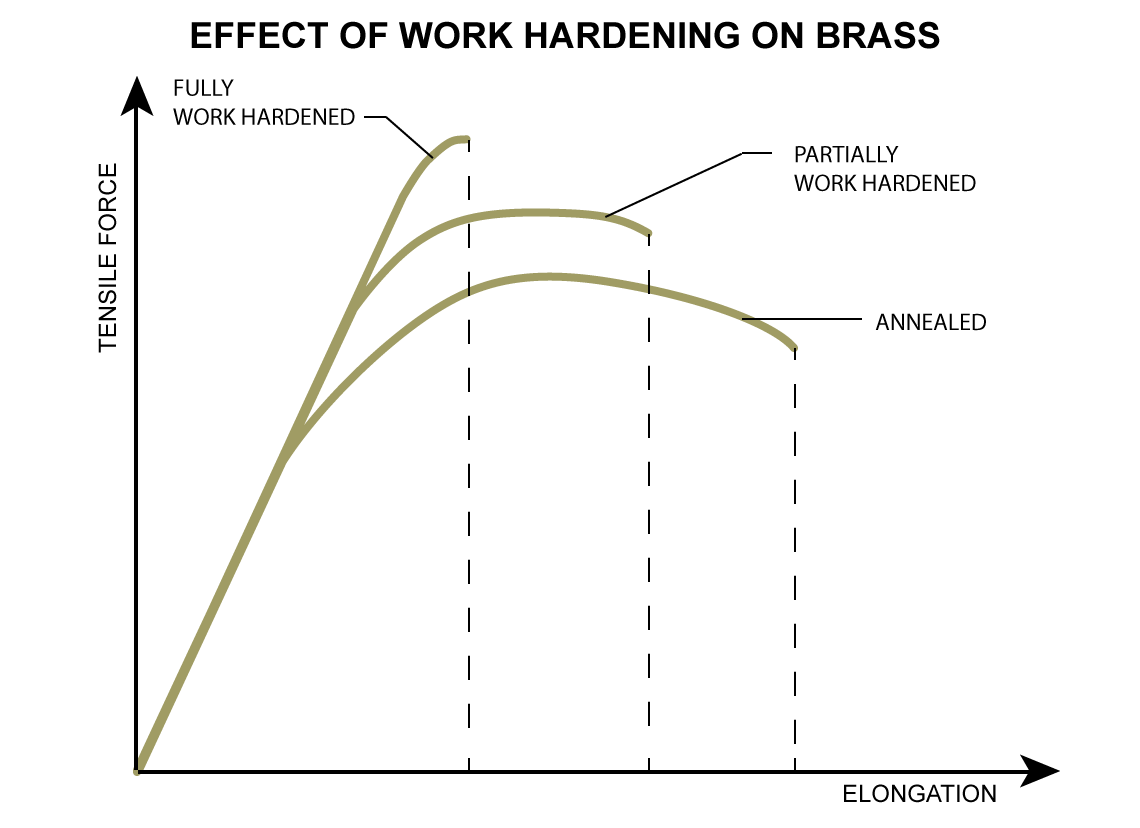
It matters because of stress and strain. Stress is the amount of force per unit of area applied to an object, like a piece of metal. If you pull on a bar with a force of 100 pounds, and the bar has a cross sectional area of 2 inches, you have applied a stress of 100 / 2 = 50 psi. Material strength is measured in units of stress (psi). Up to a certain stress level, any force you apply to a metal will spring back completely. This is known as elastic deformation. Once you hit a specific stress level known as the yield point, you will begin to deform the metal permanently. This is called plastic deformation. The stress level at which the metal goes plastic is called the yield strength. The yield strength varies considerably with the hardness of the brass (it's higher for hard brass).

Strain is the amount of deformation an object experiences under stress, expressed as a percentage of its original length. Strain equal to 0.01 means the material has grown longer by 1%.

In the elastic region, stress is linearly proportional to strain and completely reversible. If we remove the force, the material will return to it's original shape. This is known as "spring-back". The amount of stress required to produce a unit of strain is known as the elastic modulus (sometimes called Young's modulus). The elastic modulus is different for different metals. A high modulus means the material is stiff. Steel's modulus is roughly three times that of aluminum, and twice that of brass, for example.

Once you cross the yield point, you begin to add plastic strain to the elastic strain. The plastic portion will not spring back. It's permanent. The elastic portion, however, will still spring back even if you have crossed the yield point. Above the yield point, the relationship between stress and strain is no longer linear - the elastic modulus is no longer valid. After the yield point, it takes much less stress (and therefore holding force) to produce a unit of strain. Keep all of this in mind as background for what's next - an analysis of the stress in a case neck due to seating a bullet.

Neck Tension Expressed as Stress

Stress can be calculated in many ways for many different shapes and loading scenarios. You'll want to go to engineering school to learn all there is to know about that, but we'll skip that part and just give you the answer. For a case neck, we can calculate the stress as

$$\sigma = {En \over c-n}$$

where n is the neck tension, c is the bullet caliber, and E is the modulus of elasticity. If we rearrange this equation, we can find the neck tension as a function of stress:

$$n = {c\sigma \over E+\sigma}$$

What interested me was the question "how much neck tension does it require to yield the case neck?" According to the above equation, it should be dependent on both the caliber and amount of neck tension. Experience tells me that even 0.002" will generally be enough permanently deform a case neck. But what does the math tell us?

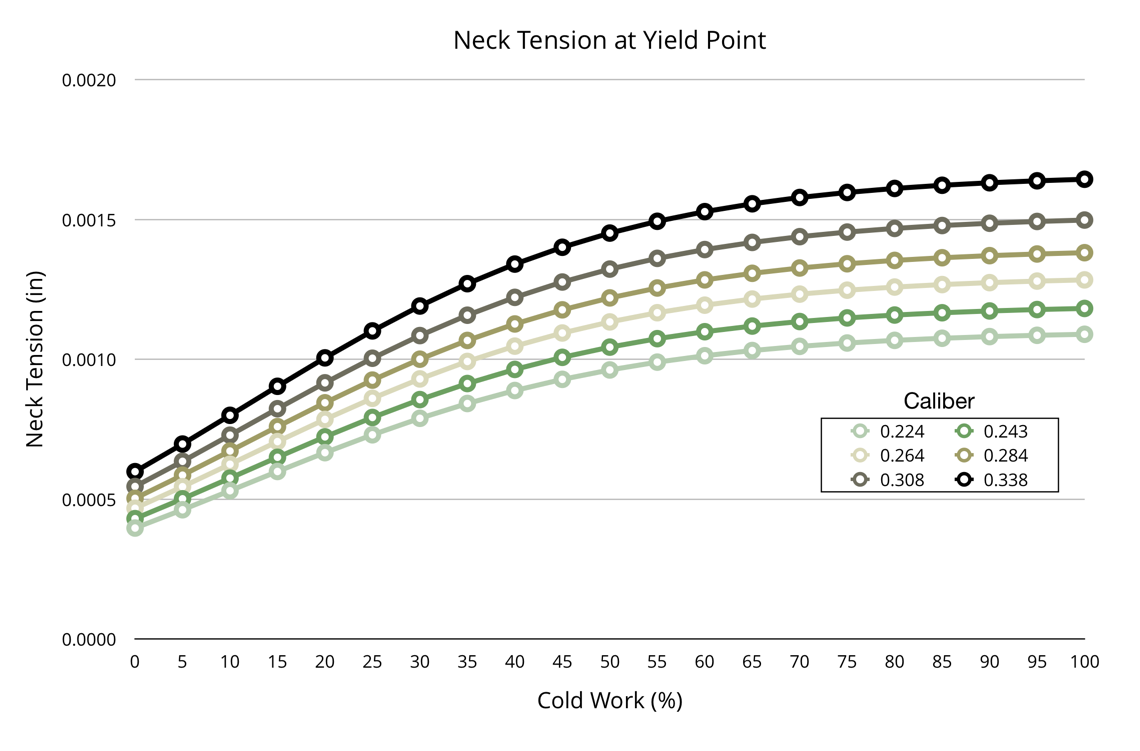
The above chart shows the neck tension at the yield point at varying stages of hardness. The bottom axis is the percentage of cold working, which is a way of describing the hardness of the brass. Extremely hard brass will have a high percentage, while dead soft fully annealed brass will have a very low percentage. "Half hard" brass is 50%, and level that many people try to hit with their annealing practices.

As you can see, it does not take much neck tension to yield the case neck. With a .30 caliber bullet and hard brass, we hit it around 0.0015" of neck tension. .22 caliber bullets can only handle .001" of neck tension before yielding.

So what?

So what does this actually mean? It means that unless you are using a very light neck tension and not annealing, you are plasticly deforming your brass when you seat a bullet.

If you do not plastically deform your brass, the amount of force holding the bullet will be very consistent because the elastic modulus is very consistent and does not vary with brass hardness. If you do plastically deform your brass, and the yield point varies at all from case to case, you will introduce variation into your holding force because of the nonlinear relationship between stress and strain above the yield point.

So how do we achieve consistent holding force? One way would be to use harder necks and very low neck tension, and thus stay in the elastic region. Another would be to use carefully annealed necks and any amount of neck tension. If you use a neck tension above the yield point, you must be very consistent in your annealing practices or you will introduce variation in your holding force.

This explains why shooters have such disagreement about the value of annealing as it pertains to neck tension. How you anneal matters, and I would argue that not annealing is a viable option since the yield point is more consistent at higher hardness levels.

Theory vs Practice

The above is all theoretical, obviously. It's very sound theory based on well known mechanical engineering practice, but as with all engineering, reality creeps in a little at the edges. In reality there are factors that make things a little more complex. The above numbers are close to reality, but not exact.

Other practical concerns pop up as well. Staying below the elastic limit means using what most shooters consider to be very light neck tension - maybe even too light to reliably hold the bullet. While this may be fine for certain rifle setups (like benchrest), it's not acceptable for hunting or PRS competition.

In the end, we still have to test every aspect of our reloading practices that we think matter. I've laid out a case for how annealing impacts neck tension and how one might take steps to use annealing in the most productive manner possible. That insight does not alleviate our needs for testing, however. It merely guides our efforts.

Damon Cali is the creator of the Bison Ballistics website and a high power rifle shooter currently living in Nebraska.